785. Is Graph Bipartite?

LeetCode 0785. Is Graph Bipartite?

---

Problem:

Given an undirected graph, return true if and only if it is bipartite.

Recall that a graph is bipartite if we can split its set of nodes into two independent subsets A and B, such that every edge in the graph has one node in A and another node in B.

The graph is given in the following form: graph[i] is a list of indexes j for which the edge between nodes i and j exists. Each node is an integer between 0 and graph.length - 1. There are no self edges or parallel edges: graph[i] does not contain i, and it doesn't contain any element twice.

Example 1:

Input: graph = [[1,3],[0,2],[1,3],[0,2]] Output: true Explanation: We can divide the vertices into two groups: {0, 2} and {1, 3}.

Example 2:

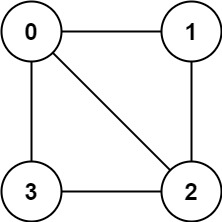Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]] Output: false Explanation: We cannot find a way to divide the set of nodes into two independent subsets.

Constraints:

• 1 <= graph.length <= 100
• 0 <= graph[i].length < 100
• 0 <= graph[i][j] <= graph.length - 1
• graph[i][j] != i
• All the values of graph[i] are unique.
• The graph is guaranteed to be undirected.

---

Solution:

The so-called bipartite graph means that all vertices in the graph can be divided into two disjoint sets so that the vertices of the same set are not connected. The general idea is to dye the two connected vertices with different colors. Once found in the dyeing process, the two adjacent vertices have been dyed the same color, indicating that it is not a bipartite graph. Here we use two colors, represented by 1 and -1, respectively. Initially, each vertex is represented by 0 for undyed, and then each vertex is traversed. If the vertex has not been visited, and the recursive function returns false, it returns false, not a bipartite graph. If false is not returned before the loop exits, return true. In the DFS function, after the current vertex was dyed, if the vertex color is the same as the color to be dyed, it returns false. Otherwise, it returns true after recursively check the unvisited node without any false return.

Time complexity:
Space complexity:

Python

class Solution:
    def isBipartite(self, graph: List[List[int]]) -> bool:
        colors = [0] * len(graph)
        
        def dfs(node, color):
            colors[node] = color
            for neighbor in graph[node]:
                if colors[neighbor] == color: 
                    return False
                if colors[neighbor] == 0 and not dfs(neighbor, -color):
                    return False
            return True
        
        for node in range(len(graph)):
            if not colors[node] and not dfs(node, 1): return False
        return True
            

Java

class Solution {
    public boolean isBipartite(int[][] graph) {
        int[] visited = new int[graph.length];
         
        for(int i = 0; i < graph.length; i ++){
            if(visited[i] == 0 && !dfs(graph, visited, i, 1)) return false;
        }
        return true;
    }
    private boolean dfs(int[][] graph, int[] visited, int curr, int color){
        visited[curr] = color;
        for(int node: graph[curr]){
            if(visited[node] == color) return false;
            if(visited[node] == 0 && !dfs(graph, visited, node, -color)) return false;
            }
        return true;
        }
}